BASIC-Kurs: "Von Adam und Eva..." (Teil 5)
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Herzlich Willkommen beim fünften Teil unseres Basic-
kurses. Wie letzten Monat schon versprochen geht es
diesmal um das sogenannte Binärsystem und den Spei-
cheraufbau unseres 64ers. Dieses Thema hat eigentlich
mit BASIC im allgemeinen ganz und garnichts zu tun,
doch ist es unerläßlich wenigstens einige Kenntnisse
davon zu haben, wenn man sich mit der Grafik- und
Soundprogrammierung auf dem C64 beschäftigen möchte.
Zunächst einmal eine kleine Erläuterung zu Zahlen im
allgemeinen:
Wie Sie ja wissen benutzen wir Menschen ein Zahlensy-
stem mit dessen Hilfe wir Maße, Gewichte, Geldsummen
oder ähnliches bequem ausdrücken können. Ich spreche
vom sogenannten "Dezimalsystem". Indem wir uns der
Ziffern 0123456789 bedienen, können wir durch belie-
biges kombinieren dieser Ziffern Zahlen von unendli-
cher Länge bilden. Ein Beispiel wäre da die Zahl
1989. Sie gliedert sich in 4 Teile auf, die ich Ihnen
im Folgenden einmal grafisch darstellen möchte:
Die Buchstaben
T,H,Z und E
stehen für
"Tausender",
"Hunderter",
"Zehner" und
"Einer". Das
heißt also, daß
die Zahl 1989
in eine Zahl
mit vier Kompo-
nenten aufge-
spaltet wird.
Mathematisch läßt sich das folgendermaßen ausdrücken:
1000*T + 100*H + 10*Z + 1*E = THZE (oder auch)
10↑3*T + 10↑2*H + 10↑1*Z + 10↑0*E = THZE
Oder in unserem Beispiel:
1000*1 + 100*9 + 10*8 + 1*9 =
10↑3*1 + 10↑2*9 + 10↑1*8 + 10↑0*9 =
1000 + 900 + 80 + 9 = 1989
Jeder Stelle der Zahl ist also eine Potenz von 10
zugeordnet (1=10↑0, 10=10↑1, 100=10↑2, 1000=10↑3,
usw...). Daher auch der Name DEZIMALsystem - "decum"
kommt aus dem lateinischen und heißt "zehn".
Dieses Verfahren läßt sich natürlich auch bei größer-
stelligen Zahlen anwenden. Bei der Zahl 2313660 ist
die höchste Zehnerpotenz 10↑6. Hierbei ist übrigens
noch anzumerken, daß die letzte Ziffer eine Null ist,
bei der der ihr zugehörige Potenzfaktor (hier 10↑0)
sozusagen "wegmultipliziert" wird, denn 1*0=0, wes-
halb auch hier als Endsumme aller Produkte der Poten-
zen 2313660 herauskommt. Das scheint alles kompli-
zierter als es ist - wichtig ist, daß Sie begriffen
haben, daß eine Dezimalziffer nur aus der Addition
von 10er-Potenzen besteht.
Sie sehen auch, daß jedesmal nachdem wir die höchste
Ziffer einer Potenz erreicht haben, nämlich die 9,
die nächste Zahl als ein Vielfaches der nächsthöheren
Potenz darstellen können. Haben Sie also die Zahl
neun erreicht, so findet ein sogenannter "Überlauf"
statt, das heißt, daß die nun folgende Zahl eine
Stelle mehr bekommt, und ihre höchste 10er Potenz mit
der Ziffer 1 als Multiplikator versehen wird. Der
Nachfolger von 9 ist 10 wobei letztgenannte Zahl eine
zweistellige ist, erstere allerdings nur eine ein-
stellige.
Ebenso kommen Überläufe vor, wenn wir von 19 auf 20
zählen. Hier wird der Zähler der nächsten Potenz um
eins erhöht. Auch von 29 auf 30 verhält es sich so,
und so fort. Bei jedem Überlauf erhält also die nied-
rigere Potenz die Ziffer 0 in den Zähler, während
die höhere die nächst höhere Ziffer verpasst bekommt.
Beim Zählen von 99 auf 100 zum Beispiel geschieht
dies sogar gleich zweimal. Zum Einen erhalten die
"Einer" (10↑0) die Nullziffer und es findet ein Über-
lauf zu den "Zehnern" (10↑1) statt, zum Anderen be-
wirkt dieser wiedrum, daß die "Zehner" überlaufen und
somit den Zähler 0 erhalten, wobei die "Hunderter"
(10↑2) um 1 erhöht werden und nun die Ziffer 1 dort
im Zähler steht.
Sehen Sie hier das Ganze ein wenig grafisch aufge-
macht (denn ein Bild sagt mehr als tausend Worte):
Wir haben also gelernt, daß die 10 mit ihren Potenzen
die Basis unseres Zahlensystems liefert, da alle De-
zimalzahlen als Summe von 10er-Potenzen dargestellt
werden können. Sie werden jetzt fragen:
"Was hat das Ganze denn mit dem Binärsystem zu tun,
darum geht es hier doch?"
Nun, das Binärsystem folgt nämlich (fast) genau die-
sem Muster, mit dem einzigen Unterschied (daher auch
die Einschränkung eben), daß wir hier nicht mit einer
Basis von 10 sondern mit der von 2 arbeiten. Auch
hier können Sie den Namen des Systems von ihr ablei-
ten "Bi" steht für Zwei. Da wir ja nun alle 2er-
Potenzen verwenden, brauchen wir logischerweise auch
nur zwei Ziffern, mit denen wir unsere Binärzahlen
darstellen (im Dezimalsystem hatten wir ja 10 davon -
Sie sehen, es werden immer soviele Ziffern benötigt,
wie die Basis angibt). Dies sind ganz einfach die
Ziffern 0 und 1. Demnach kann man also sagen, daß
eine Binärzahl so aussehen könnte: 11001010. Diese
hier zum Beispiel ist achtstellig. Das hat einen be-
sonderen Grund, wie wir später erkennen werden.
Wie sich eine solche Zahl jetzt zusammensetzt ist
klar - wir müssen ganz einfach die Potenzen von 2
nebeneinander schreiben (allerdings mit der niedrig-
sten ganz links und der höchsten ganz rechts) und die
Produkte der Binärziffern mit den ihnen zugehörigen
Potenzen miteinander addieren. Als Ergebnis erhalten
wir dann unsere Binärzahl in Dezimalschreibweise.
Führen wir dies doch einmal durch:
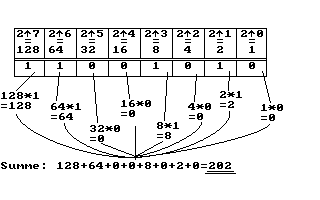
Sie sehen also: wir benutzen hier genau dasselbe
Prinzip wie beim Dezimalsystem, mit dem Unterschied,
daß hier die Produkte der 2er-Potenzen addiert wer-
den.
Doch warum das alles? Wozu können wir das Binärsy-
stem gebrauchen, und warum sind achtstellige Binär-
zahlen etwas Besonderes? Leider muß ich zur Beant-
wortung dieser Frage wiederum etwas weiter ausholen:
Im Prinzip kann man sagen - und das wird mir jeder,
der sich mit Computern gut auskennt bestätigen:
"Computer sind dumm".
Sie können nämlich ausschließlich nur zwischen
"STROM AN" und "STROM AUS" unterscheiden. Das heißt,
daß sie nur erkennen können, ob auf einer ihrer vie-
len Leitungen ein elektrischer Strom fließt, oder
nicht. Was Computer jetzt allerdings so schlau macht,
daß wir Ihnen Befehle eingeben können, die sie dann
ausführen können liegt einfach nur daran, daß sie
immens viele socher EIN/AUS-Leitungen besitzen und
daß diese in richtiger Kombination bestimmte Wirkun-
gen erzielen können. Ein recht einfaches Beispiel
wäre etwa folgendes:
Angenommen, ein Computer hätte vier Leitungen vor
sich, die er auf EIN oder AUS überprüfen könnte. Er
erkennt, daß Leitung 1 EINgeschaltet (sprich: "auf
ihr fließt Strom), Leitung 2 AUSgeschaltet (hier
fließt also KEIN Strom), Leitung 3 wieder EINgeschal-
tet und Leitung 4 ebenfalls wieder EINgeschaltet
sind. Daraus ergibt sich die Kombination:
EIN
AUS
EIN
EIN
Nun weiß unser Computerchen zusätzlich noch, daß er,
wenn diese Kombination eintreten sollte, beispiels-
weise die Hintergrundfarbe auf Dunkelgrau umschalten
soll. Diese Information ist irgendwo in seinem Aufbau
gespeichert.
Sie sehen also, so einfach (oder kompliziert) ist es,
einen Computer ganz elementar zu programmieren, das
heißt also ganz grundsätzlich, ohne irgendwelche
Hilfsmittel ihm einen Befehl zu erteilen, indem man
bestimmte Stromleitungen in ihm ein- oder ausschal-
tet. Kompliziert ist dies vielleicht deshalb, weil
man hierzu alle möglichen Kombinationen mit ihrer
Wirkung kennen muß. Das sind bei vier Leitungen zwar
"nur" 16 verschiedene, aber es könnten ja beispiels-
weise auch viel mehr Leitungen zum Unterscheiden zur
Verfügung stehen.
Hm - Moment einmal, die Zahl 16 hatten wir doch heute
schon einmal!!! Genau - 16 ist die vierte Potenz von
2 (also 2↑4), der Wert der fünften Ziffer des
Binärsystems! Und genau das ist es, worauf ich hin-
aus möchte: die oben genannte EIN/AUS-Kombination
könnte nämlich auch genausogut folgendermaßen ausse-
hen (wenn man anstelle von EIN die Ziffer 1 und an-
stelle von AUS die Ziffer 0 schreibt):
EIN AUS EIN EIN
1 0 1 1
Und siehe da: da haben wir doch eine echte (vorläu-
fig vierstellige) Binärzahl! Ins Dezimalsystem umge-
rechnet lautet sie übrigens 11 (elf). Und tatsächlich
ist es auch so, daß wenn wir unserem C64 an einer
bestimmten Stelle in seinem Speicher die Zahl 11 an-
geben, er den Bildschirm in die Farbe Dunkelgrau um-
färben wird. "An einer bestimmten Stelle" hört sich
vielleicht etwas merkwürdig an, doch werden wir dies
jetzt noch klären.
Wollen wir uns nun mit dem Speicheraufbau unseres C64
befassen. Anschließend werden Sie feststellen, daß
das Wort "Stelle" absolut passend ist.
Wie Sie vielleicht einmal gehört haben, oder in Ihrem
C64 Bedienungshandbuch gelesen haben, verfügt Ihr
kleiner Freund über 64 (sogenannte) Kilobytes (Abkür-
zung : KB) Speicher (bei denjenigen Lesern, die die
Funktionsweise des Binärsystems begriffen haben soll-
ten, müßte eigentlich gerade eben ein Licht aufgegan-
gen sein - 64 ist die sechste Potenz von 2, also
2↑6). Bestimmt konnten Sie bis jetzt absolut nichts
damit anfangen, weshalb wir jetzt erst einmal klären
wollen was ein Kilobyte, oder besser ein einzelnes
Byte ist. Zuerst einmal zum Byte:
Ein Byte ist die Zusammenfassung von acht(!) soge-
nannten Bits. Man kann also sagen: 1 Byte = 8 Bits.
Doch was, um alles in der Welt, ist jetzt wieder ein
Bit? Nun, ein Bit ist ganz einfach eine von jenen
vielen Leitungen, wie ich sie oben schon beschrieben
hatte, die ein- und ausschaltbar sind. Eine von die-
sen Leitungen, die ein Computer miteinander kombi-
niert, um den Befehl, den er ausführen soll zu ermit-
teln. Womit unsere Frage nach dem "Warum eine acht-
stellige Binärzahl" beantwortet wäre: da unser Bit
für eine stromführende Leitung steht, die entweder
EIN- oder AUSgeschaltet sein kann (1 oder 0) , und
weil acht Bit einem Byte entsprechen, kann dieses
Byte mit Hilfe einer achtstelligen Binärzahl aus-
gedrückt werden. Man spricht hier von dem "Wert" ei-
nes Bytes. Von der Binärzahl also, die in diesem Byte
enthalten ist, oder anders gesagt: von den Bits, die
in diesem Byte "gesetzt" (Bit=1) oder "nicht gesetzt"
(Bit=0) sind.
Würde man also sagen: dieses Byte hat den Wert 202,
so würde man damit die Bitgruppe 11001010 meinen
(hier einmal die Werte unseres Beispiels von oben).
Ein Kilobyte ist jetzt ganz einfach die Gesamtheit
von 1024 Bytes. Dies verhält sich etwa ähnlich wie
bei Gramm und Kilogramm. Ein Kilogramm sind 1000
Gramm, oder das 10↑3-fache von 1. Bei Bytes rechnet
man mit einer Potenz von 2, da die Bytes ja auch auf
ein System aus 2er-Potenzen aufgebaut sind, und somit
die Zahlen besser "harmonieren". Doch dies ist jetzt
unwichtig, da Sie die Bedeutung dieser "Harmonie"
erst verstehen müssen, wenn Sie einmal die Maschi-
nensprache (auch "Assembler genannt) lernen werden.
Des Weiteren sind ein Megabyte demnach also 1024 Ki-
lobytes. Am Rande vielleicht eine kleine Umrechnung-
stabelle:
1 Megabyte = 1024 Kilobytes = 1024*1024 Bytes
(1024*1024 sind übrigens 1048576, also "ein klein
wenig" mehr als eine Million...)
Jetzt wissen Sie also, daß wir insgesamt 64*1024*8
(=524288) Leitungen in unserem C64 haben (64 KB
eben), die alle in verschiedenster Weise ein- oder
ausgeschaltet sein können. Zahlenmäßg gesehen ist das
ja eine ganz schöne Menge, in der Realität werden wir
allerdings nur eine Handvoll davon effektiv nutzen
können. Man kann etwa sagen, daß gute 99 Prozent die-
ser 64 Kilobytes nur zur Speicherung von Befehlen
benutzt wird. Das heißt also, daß sich der Computer
in diesen Bereichen die Befehle, die er irgendwann
einmal ausführen soll, einfach nur zwischenspeichert,
damit er sie bei Bedarf dann gleich griffbereit hat,
um sie abzuarbeiten. Doch dies fällt ebenfalls in den
Themenbereich der Maschinensprache, wo es sogar eine
sehr große Rolle spielt.
Diese 65536 Bytes (=64 KB), können jetzt alle einzeln
mit ihren Nummern angesprochen werden. Bildlich könn-
te man sich das etwa wie eine Straße vorstellen, in
der es 65536 Häuser gibt, mit ebenso vielen Hausnum-
mern. Möchten Sie jetzt beispielsweise einen Brief an
das Haus mit der Nummer 53281 schicken, so müßten Sie
diesen an folgende Adresse schicken:
An
Herrn Byte
Speicherstraße 53281
64KB Commodore 64
Der Name des Adressaten und der adressierten Stadt
dient hier nur zur Untermalung, wichtig ist jedoch,
daß Sie erkennen, daß Sie so einen "Brief" an das
Haus mit der Nummer 53281 schicken können. Der Inhalt
dieses Briefes könnte etwa folgendermaßen aussehen:
Sehr geehrter Herr Byte,
00001011
Herzlichst, Ihr Programmierer.
Auch diesmal nur ein kleines aufmunterndes Beispiel,
um den Zweck des "Verschicken eines Briefes" aufzu-
zeigen. Tatsächlich sagt man sogar, daß man ein Byte
"adressiert", also seine "Adresse" angibt, und ihm
dann einen Wert zuweist. Mit unserem Brief hätten wir
also dem Byte 53281 den Wert 00001011 zugewiesen,
womit wir wieder beim Binärsystem wären. Der aufmerk-
same Leser hat bestimmt schon längst gemerkt, daß wir
hier die Binärzahl von vorhin auf dem Bildschirm ste-
hen haben, nämlich die dezimale 11. Diesmal aller-
dings achtstellig, da wir ja gelernt haben, daß man
das ganze Byte adressiert, und somit auch auf jeden
Fall 8 Bits verändert. Die höherwertigen 4 Bits bein-
halten jetzt ganz einfach die Ziffer 0, womit ihre
Produkte mit ihren jeweiligen Potenzen auch zu 0 wer-
den, weshalb sie auch nicht zu Gewicht schlagen.
Wollen wir nun endlich den BASIC-Befehl kennenlernen,
mit dem wir "Briefe verschicken" können: der POKE-
Befehl.
Die Syntax von POKE ist denkbar einfach: Sie müssen
hinter dem Befehlswort POKE ganz einfach nur noch die
Adresse des zu verändernden Bytes angeben und an-
schließend, durch ein Komma voneinander getrennt, den
Wert, der zugewiesen werden soll, allerdings in dezi-
maler Schreibweise. Daher also auch die vorangehende
langwierige Erklärung des Binärsystems, denn später
müssen Sie sich Ihre Bitkombinationen selbst zusam-
menrechenen können.
Um unser Adressierungsbeispiel gleich in die Realität
umzusetzen - hier ist der Brief an Herrn Byte, wie
wir ihn in BASIC schreiben mÜssten:
POKE 53281,11
Wir haben also der Speicherzelle (das ist die deut-
sche Übersetzung für Byte) 53281 den Dezimalwert 11
beziehungsweise den Binärwert 00001011 zugewiesen.
Probieren Sie es doch einmal aus, und beobachten Sie,
was passiert... Na? Verblüfft? Eben genau DAS ist
eingetreten, was ich Ihnen vorhin beschrieben hatte:
der Hintergrund des Bildschirms Ihres C64 hat sich
vom üblichen Blau in ein tristes Dunkelgrau verfärbt.
Sie sehen also, man muß nur die richtigen STELLEN im
Speicher des 64ers verändern, um gewisse Ergebnisse
zu erzielen.
Jetzt möchte ich Ihnen allerdings nicht verschweigen,
daß es ebenso möglich ist, von einer Speicherzelle
einen Brief zu erhalten. Das heißt also, daß Sie als
Programmierer die Speichezelle dazu veranlassen kön-
nen, ihren Inhalt (oder ihren Wert) Ihnen zuzuschik-
ken. Dies kann in BASIC mit der PEEK-Funktion reali-
siert werden. Die Syntax von PEEK ist ebenfalls sehr
einfach: Sie müssen nach dem Befehlswort PEEK nur
noch die gewünschte Byteadresse, in Klammern gesetzt,
angeben, um den Inhalt dieses Bytes zu erhalten. Ich
möchte darauf aufmerksam machen, daß es sich hierbei
um eine FUNKTION handelt. Sie können PEEK also ohne
alles kaum effektiv nutzen, es solte nämlich schon
ein PRINT-Befehl, eine Variablenzuweisung, oder ein
Vergleich durch IF-THEN dabei stehen, um der Funktion
entsprechend einen Sinn zu geben. Eine Möglichkeit,
sich den Inhalt einer Speicherzelle anzusehen, wäre
über PRINT gegeben. Versuchen Sie doch einmal folgen-
des:
PRINT PEEK(53281)
Jetzt sollten Sie eine Zahl auf dem Bildschirm stehen
haben. Sie gibt die Farbe des Hintergrundes an, da
das Byte 53281 ja für die Farbe des Bildschirms
zuständig ist, wie wir es vorhin gelernt hatten. Es
kann durchaus sein, daß Sie jetzt hier etwas anderes
als 11 auf dem Bildschirm stehen haben. Das hat etwas
mit der computerinternen Handhabung der Farben zu
tun, doch das wollen wir an späterer Stelle genauer
behandeln. Prinzipiell kann man jetzt also sagen, daß
Sie mit Hilfe von PEEK und POKE ein Byte zu verschie-
denen Aktionen veranlassen können. Mit PEEK lassen
Sie sich von dem Byte einen Brief schicken, der sei-
nen Wert beinhaltet und mit POKE können Sie das Spiel
umkehren und dem Byte einen Brief zuschicken, der den
Wert beinhaltet, den es annehmen soll. Wie wir gese-
hen haben, ist gerade letztere Funktion ja sehr nütz-
lich, wenn wir verschiedene Dinge im Computer bewir-
ken wollen, man muß nur wissen an welchen Stellen man
Änderunngen vornehmen muß, um einen gewissen Effekt
zu erzielen.
Womit wir wieder bei den Stellen wären. Ich möchte
Ihnen hier einmal eine kleine Übersicht aller Stellen
(Bytes, Speicherzellen, Hausnummern, Adressen, oder
wie Sie es auch immer nennen möchten) geben, wie Sie
im C64 vorkommen. Man kann diese 65536 Bytes nämlich
in gewissen Aufgabenbereichen zusammenfassen, um et-
was Ordnung in die Tausenden von verschiedenen Zellen
zu bringen:
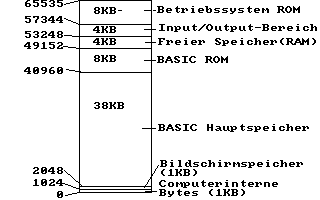
Ich habe hier den Speicher des C64 einmal mit Hilfe
eines Balkens, der in verschiedene Teilbereiche auf-
gespalten ist, dargestellt. Unten sehen Sie die Spei-
cherzelle 0, und am oberen Rand haben wir das letzte
Byte, mit der Adresse 65535. Sie werden jetzt fra-
gen: "Warum 65535 wo wir doch die ganze Zeit von
65536 Bytes reden ?" - Nun, wir müssen hier wieder
berücksichtigen, daß das Byte mit der Adresse 0 ja
auch mitzählt, somit haben wir (rein zahlenmäßig)
dann 65535 Bytes plus ein 0-Byte, das macht
65535+1=65536!
Ich möchte Ihnen hier dann gleich noch die Aufgaben
der verschiedenen Speicherbereiche erläutern, wie ich
sie im Bild schon angedeutet habee. Hierbei möchte
ich allerdings vorerst die Bytes von 0 bis 40960
übergehen, da Sie deren Funktionsweise besser verste-
hen können, wenn Sie die der Folgenden schon kennen.
Beginnen wir also bei 40960 bis 49152. Hier steht das
sogenannte BASIC-ROM. Klären wir zunächst einmal,
wofür ROM steht. Hierzu sollte ich vielleicht erwäh-
nen, daß es zwei verschiedene Arten von Speicherzel-
len in Ihrem C64 gibt. Bestimmte Teilbereiche haben
also bestimmte Eigenschaften, die ein anderer wiede-
rum nicht hat. Die zwei Arten, von denen hier gespro-
chen wird, nennt man RAM und ROM. RAM steht für "Ran-
dom Access Memory" und ROM für "Read Only Memory".
Übersetzen wir dies aus dem Englischen, so haben
wir: "Speicher für beliebigen Zugriff" und "Spei-
cher, der nur gelesen werden kann." Dies heißt im
Klartext, daß RAM-Speicherzellen beschrieben UND ge-
lesen werden können, im Gegensatz zu ROM-Adressen,
die NUR gelesen werden. Sie können sich dies etwa mit
folgendem Bild verdeutlichen: die RAM-Adressen sind
schreibfreudige Mitbürger. Sie erhalten gerne Briefe,
und beantworten diese auch, sollten sie dazu aufge-
fordert worden sein. ROM-Adressen hingegen sind eher
Kontaktscheu, sie ignorieren ihre Post, und werfen
sie, wie Sie es vielleicht auch manchmal bei Werbe-
sendungen tun, ungelesen in den Mülleimer. Sie kennen
ihren Programmierer schon gut genug, weshalb sie auch
nur dann an ihn ihren Inhalt senden, wenn dieser es
unbedingt verlangt. Außerdem sind ROM-Adressen sehr
konservative Individuen, sie haben nämlich auch gar
nicht vor, ihre Einstellung (also ihren Wert) zu än-
dern und bleiben auch auf Immer und Ewig bei ihrem
voreingestellten Wert.
Doch jetzt einmal Spaß beiseite - der Grund, warum
man ROM und RAM schuf, war einfach der, daß man einen
Speicher benötigte, der auch ohne Stromzufuhr, also
im ausgeschalteten Zustand des Computers, in der Lage
ist, seine in ihm gespeicherten Informationen zu be-
halten. Da man sonst bei jedem neuen Einschalten ei-
nes Computers ein gewisses Grundprogramm jedesmal
wieder von Neuen hätte eingeben müssen, wobei natür-
lich die Frage aufkommt, wie man dies getan hätte, da
in einem leeren Computer ohne Programm auch nichts
getan werden kann, um Daten aufzunehmen, da dieser
immer ein Programm braucht, das ihm diese Daten ein-
liest. Ebenso ist es bei BASIC. In dem vorhin ange-
sprochenen Bereich des BASIC-ROMs sind die Grundpro-
gramme gespeichert, die es uns ermöglichen, in BASIC
mit unserem 64er zu kommunizieren. Alle Befehle, die
wir bisher behandelt haben, ebenso wie diese, die
noch kommen werden, sind hier genauestens definiert,
so daß der Computer immer genau weiß, was er zu tun
hat, wenn Sie ihn Beispielsweise mit der Buchstaben-
folge PRINT konfrontieren.
ROM braucht also keinen Strom, um die in ihm gespei-
cherten Bits zu behalten. Sie können sich dies etwa
als eine Unmenge von Leitungen vorstellen, die fest
und unveränderlich sind. Und nicht, wie es beim RAM
der Fall ist, durch Schalter ein-, oder ausschaltbar
sind. ROM-Bits STEHEN ganz einfach schon auf EIN oder
AUS.
Der Vorteil am RAM ist ganz einfach, daß man seinen
Inhalt sozusagen "von Hand" verändern kann und wäre
dies nicht möglich, so könnte man beispielsweise die
Bildschirmfarbe auch gar nicht verändern. Dafür geht
diese dann allerdings auch verloren, wenn man die
Stromzufuhr unterbricht.
Doch machen wir nun wieder in unserer Speicherüber-
sicht weiter. Es folgt nun der Bereich von 49152 bis
53248. Hier ist freier RAM-Speicher, der vom Computer
nicht benutzt wird. Wir als Programmierer, können ihn
uns zwar zu Nutze machen, doch das ebenfalls erst,
wenn Sie sich einmal mit Assembler befassen sollten.
Der folgende Speicherbereich ist der für uns BASIC-
Programmierer wichtigste, weshalb ich anschließend
auch etwas genauer darauf eingehen werde. Der soge-
nannte I/O-Bereich, oder Input/Output-Bereich (von
53248 bis 57344), enthält die Speicherzellen der ver-
schiedenen Ein-/Ausgabe-Bausteine (Input/Output =
Eingabe/Ausgabe). Das sind jene Bausteine (oder Com-
puterchips) in unserem C64, die dafür verantwortlich
sind, daß zum Beispiel der Ton aus dem Lautsprecher
kommt, daß das Floppylaufwerk auch odrnungsgemäß sei-
ne Daten speichert, oder daß, wie oben schon gezeigt,
der Bildschirm in dunkelgrauer Farbe dargestellt
wird. Wir wollen uns Speziell um zwei bestimmte Chips
aus diesem Bereich kümmern, sie tragen die Namen SID
und VIC.
SID steht für "Sound Interface Device" was etwa so-
viel heißt wie "Musikerzeuger" (nicht wörtlich über-
setzt, doch das hier trifft die Aufgabe von SID auf
den Punkt genau). Um ihn werden wir uns in einer der
nächsten Ausgaben noch kümmern.
VIC ist die Abkürzung für "Video Interface Control-
ler". Wie sein Name schon verrät (Überwacher der Vi-
deoschnittstelle, oder frei nach J.R.R. Tolkien "Der
Herr der Videoschnittstelle"), ist er zuständig für
Bildschirmaufbau und Grafik innerhalb unseres Compu-
ters. Er wird auch unser Hauptthema sein, um das es
sich nächsten Monat drehen wird.
Nun wollen wir noch unsere Speichertabelle zu Ende
abhandeln. Da wäre zunächst einmal noch der Bereich
von 57344 bis zum Ende des Speichers (also bis
65535). Hier haben wir wieder einen ROM-Bereich vor-
liegen, diesmal allerdings das Betriebssystem-ROM.
Das Betriebssystem ist der wichtigste Teil eines Com-
puters, da in ihm alle Unterprogramme enthalten sind,
die zur Steuerung des Computers beim Einschalten und
während der Eingabe über die Tastatur unbedingt not-
wenig sind. Hier liegt das eigentliche Herzstück des
C64, ohne das er nur bedingt leben könnte. Wenn wir
das aus unserer Sicht als werdende BASIC-
Programmierer betrachten, könnte er es sogar über-
haupt nicht. Hier muß ich dann abermals auf die Ma-
schinensprache verweisen, denn bei dieser ist es dur-
chaus möglich, den C64 OHNE Betriebssystem zu benut-
zen, doch ist dies auch hier nur unter -relativ- gro-
ßem Aufwand machbar. Auch werden Sie beim Erlernen
der Maschinensprache nicht umhin kommen, sich mit dem
Betriebssystem eingehender zu befassen, Sie werden es
nach einiger Zeit sogar sehr zu schätzen wissen.
Zum Abschluß noch die Speicherbereiche von 0 bis
40960, deren Funktionen Sie jetzt besser verstehen
werden:
Da wäre ja zuerst einmal der Bereich von 0 bis 1024.
In diesem Bereich findet sich eine Ansammlung von
Bytes, die ausschließlich vom Betriebssystem und von
BASIC benutzt werden, um bestimmte Werte zwischenzu-
speichern. Uns als BASIC-Programmierern bleiben die
meisten davon verschlossen, und wir können Sie nur in
bedingtem Maße für uns nutzen, doch auch dies zu ei-
nem späteren Zeitpunkt.
Dann käme als nächstes das VIDEO-RAM, oder der Bild-
schirmspeicher, von 1024 bis 2048. Auf diesen Bereich
werden wir nächsten Monat auch noch genauer eingehen,
da er, wie sich aufgrund des Namens vielleicht ja
schon vermuten läßt, etwas mit VIC zu tun hat. Hier
sei nur gesagt, daß in diesem Bereich die Zeichen,
wie sie normalerweise immer auf dem Bildschirm ste-
hen, in genau der Reihenfolge abgespeichert sind, wie
Sie sie auf diesem abgebildet sehen.
Als letztes hätten wir dann noch den Bereich von 2048
bis 40960. Zugegebenermaßen wohl der größte Speicher-
bereich im 64er. Hier werden in aller Regel die Pro-
grammzeilen, so wie Sie sie eingeben gespeichert.
Der LIST-Befehl tut also nichts anderes, als die
BASIC-Zeilen, die hier gespeichert sind, Ihnen auf
dem Bildschirm darzustellen.
In diesem Bereich finden übrigens gleichzeitig auch
alle Variablen Platz, die Sie in Ihren Programmen
verwenden.
Hiermit bin ich nun wieder am Ende der Folge ange-
langt und hoffe, Ihnen nicht zu sehr die Gehirnwin-
dungen mit der Thematik des Speicheraufbaus und des
Binärssystems verknotet zu haben. Wie Sie ja merkten,
hatten wir diesmal eigentlich kaum etwas mit BASIC
zu tun, wenn man einmal von PEEK und POKE absieht.
Doch glaube ich mit diesem Artikel bei Ihnen einen
Grundstein für das "wirkliche" Vertändnis von Compu-
tern gelegt zu haben, da Sie mit Hilfe der Informa-
tionen, die Sie hier und heute erlangt haben, sich
viele Phänomene der Informatik sehr einfach und ver-
ständlich verdeutlichen können.
Ich darf Ihnen nun noch ein fröhliches Gehirnentkno-
ten wünschen und verabschiede mich bis nächsten Mo-
nat, wenn es dann heißt "Von nun an wirds aber bunt -
die Grafikprogrammierung als solche",
Ihr Uli Basters.

